Profile picture

Postdoctoral Researcher

Inria de Saclay
91120 Palaiseau

firstname.lastname@inria.fr
Google Scholar

Bio

I am an Inria postdoctoral researcher in the Quacs group at LMF. My interests include category theory and the application of these methods to problems in physics, particularly quantum theory and models of spacetime.

I completed my DPhil at the University of Oxford. Prior to this I did an MSci in Mathematics at Imperial College London and an MRes in Quantum Technologies at University College London.

Publications

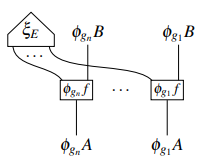
Quantum Theory Can Decohere from a Causally-Indefinite Post-Quantum Theory
With:
Preprint, 2025.
A BV-Category of Spacetime Interventions
With:
Preprint, 2025.
A Profunctorial Semantics for Quantum Supermaps
With:
Logic in Computer Science, 2024.
Optics for Premonoidal Categories
With:
Applied Category Theory, 2023.
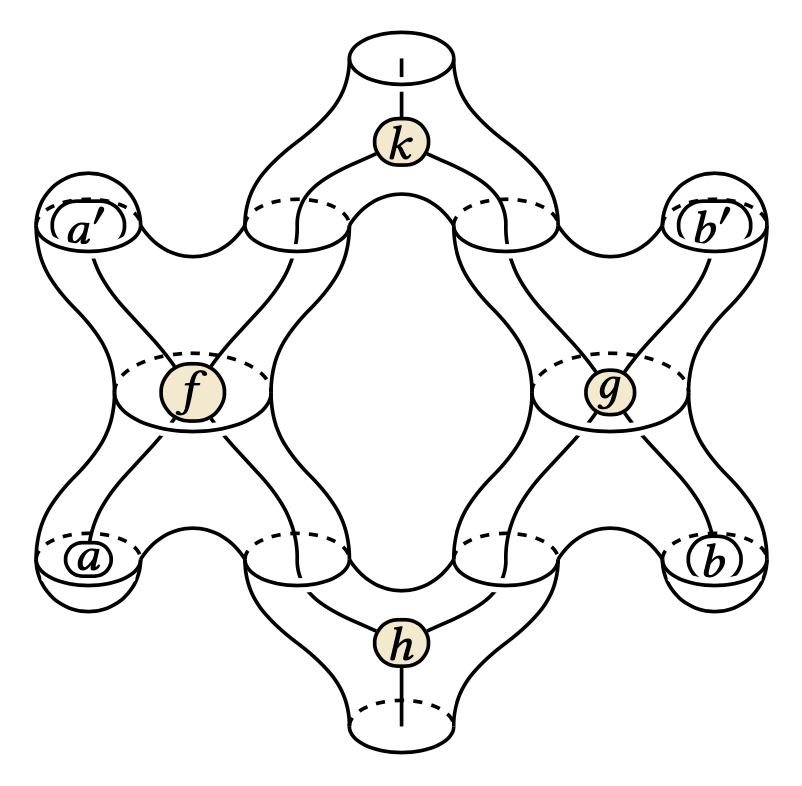
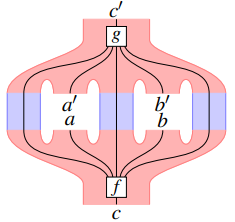
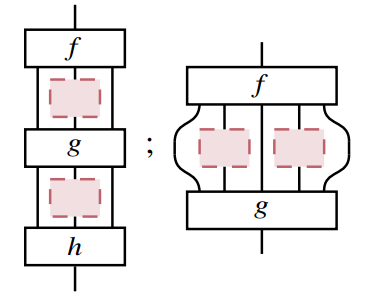
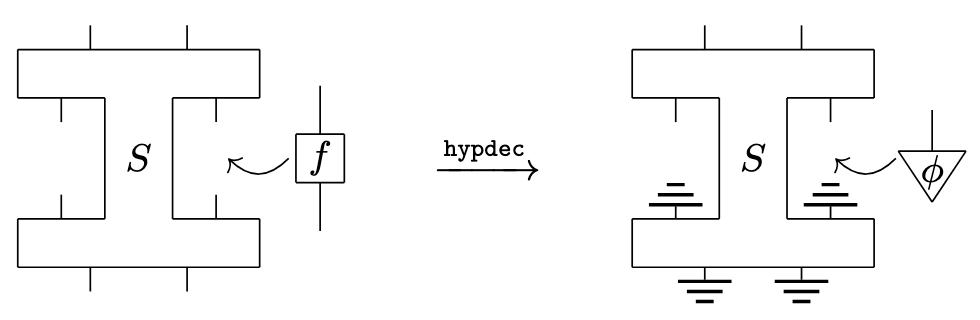
The Produoidal Algebra of Process Decomposition
With: ,
Computer Science Logic, 2024.
On the Pre- and Promonoidal Structure of Spacetime
With:
Applied Category Theory, 2022.
Coend Optics for Quantum Combs
With:
Applied Category Theory, 2022.
Optimal local unitary encoding circuits for the surface code
With: , , , , ,
In Quantum, 2021.
CPM Categories for Galois Extensions
With:
Quantum Physics and Logic, 2021.
Hyper-decoherence in Density Hypercubes
With:
Quantum Physics and Logic, 2020.